在经典的扫雷游戏中,玩家常常会遇到一个令人沮丧的情况:即使运用了所有可能的推理技巧,仍然不得不纯靠运气来选择下一步。这种"不得不猜"的设计一直是扫雷游戏最为人诟病的缺陷之一。虽然市面上已经有了一些无猜版本的扫雷实现,但我对Windows 7版本扫雷中那个经典的界面情有独钟。于是萌生了一个想法:能否在保留原版界面的基础上,将其改造成一个真正的"逻辑游戏"?
逆向工程分析
由于无法获取原版扫雷的源代码,我们需要通过逆向工程来理解和修改游戏逻辑。所幸这款游戏自带了调试符号(PDB文件),这大大简化了我们的分析工作。
使用IDA进行初步分析
使用IDA Pro打开Minesweeper.exe,IDE自动下载了对应的PDB文件。通过符号信息,我们可以直接定位到关键函数Board::Board:
__int64 __fastcall Board::Board(__int64 a1, int a2, int a3, int a4, int a5, int a6, int a7, int a8, char a9)
{
// ... 初始化代码省略 ...
if ( *(_DWORD *)(a1 + 8) > *(_DWORD *)(a1 + 12) * *(_DWORD *)(a1 + 16) - 9 )
{
v22 = Str::Str((Str *)v25, L"Too many mines for tile count");
LOBYTE(v23) = 1;
StrErr(v22, v23);
*(_DWORD *)(a1 + 8) = *(_DWORD *)(a1 + 12) * *(_DWORD *)(a1 + 16) - 9;
}
return a1;
}
通过分析反汇编代码,我们可以推断出Board类的主要结构。特别值得注意的是,代码中包含了一个边界检查,确保地雷数量不会超过(width * height - 9)个,这个"-9"正好对应着首次点击时需要预留的3×3空白区域。
深入分析地雷布置算法
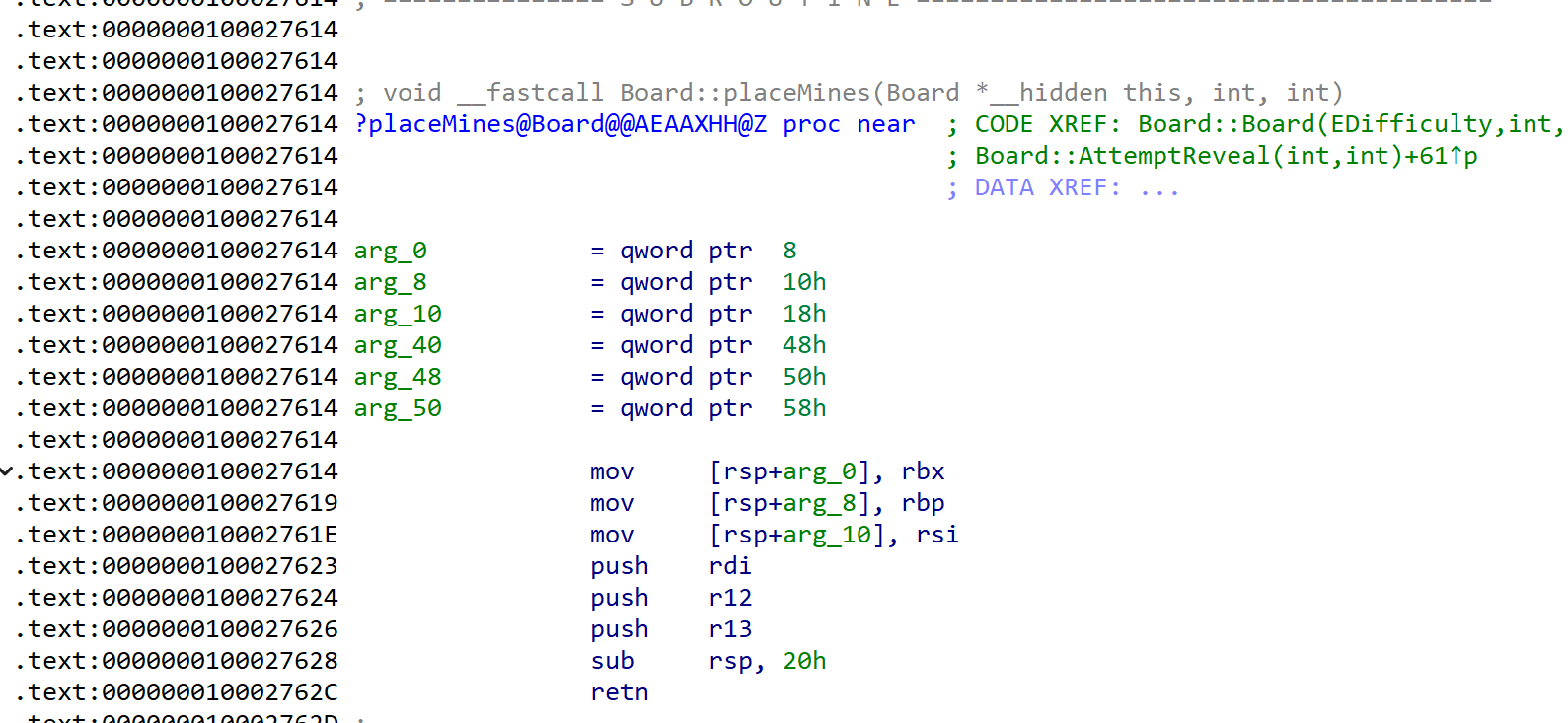
进一步分析发现,核心的地雷布置逻辑位于Board::placeMines函数中。经过分析和代码美化,其基本逻辑如下:
void Board::placeMines(int firstX, int firstY) {
// 保存当前随机种子状态
unsigned int oldSeed = Seed;
srand(this->randSeed);
Seed = this->randSeed;
// 创建可放置地雷的位置列表
Array<int>* availablePositions = new Array<int>();
// 收集所有合法的地雷放置位置
// 排除首次点击的3×3范围
for(int i = 0; i < height * width; i++) {
int x = i % width;
int y = i / width;
int dx = x - firstX;
int dy = y - firstY;
if(abs(dx) > 1 || abs(dy) > 1) {
availablePositions->Add(i);
}
}
// 随机选择指定数量的位置放置地雷
while(minePositions->size < mineCount && availablePositions->size > 0) {
int randomIndex = rand() % availablePositions->size;
int position = availablePositions->data[randomIndex];
minePositions->Add(position);
// ... 从可用位置列表中移除已选位置 ...
}
// 恢复随机种子
srand(oldSeed);
Seed = oldSeed;
}
分析这段代码,我们可以看出:
- 游戏采用线性同余随机数生成器
- 地雷布置采用简单的随机抽样策略
- 首次点击安全区域的实现是通过预先排除对应位置实现的
这种随机布置策略虽然确保了游戏的基本可玩性,但并未考虑局面是否可以通过纯逻辑推理解决,这正是导致"必须猜测"情况出现的根本原因。
静态补丁方案设计
最直接的修改方式是使用DLL注入技术,但这种方法需要额外的加载器,且会引入不必要的启动延迟,并且启动方式也不再是简单双击exe文件。 为了追求更优雅的解决方案,我决定采用静态补丁的方式,直接修改可执行文件的代码段。
首先尝试最简单的修改:将placeMines函数改为直接返回,测试我们的补丁机制是否可行:
def va2foffset(va):
"""将虚拟地址转换为文件偏移"""
image_base = pe.OPTIONAL_HEADER.ImageBase
rva = va - image_base
for section in pe.sections:
if section.VirtualAddress <= rva < section.VirtualAddress + section.SizeOfRawData:
return (rva - section.VirtualAddress) + section.PointerToRawData
return None
# 定位到placeMines函数的起始位置
place_mines_offset = va2foffset(0x100027614)
# 注入一条简单的返回指令
encoding, _ = ks.asm('ret', as_bytes=True)
with open(target_path, 'r+b') as f:
f.seek(place_mines_offset)
f.write(encoding)
测试运行游戏,果然得到了一个完全无雷的棋盘:

可以简单控制雷区的分布

这个初步的测试证实了我们的补丁机制是可行的。不过,要实现真正的无猜扫雷算法,我们需要一个更大的代码空间。原有的placeMines函数空间显然不足以容纳复杂的算法逻辑。
代码段Patch与内存管理
PE文件结构扩展
在确认了基本的补丁机制可行后,我们面临的第一个技术挑战是如何在PE文件中注入足够大的代码空间。原始的placeMines函数显然无法容纳我们的无猜算法实现。最自然的解决方案是添加一个新的节(Section)。这种方法不仅优雅,而且能够保持原有代码段的完整性。
在PE文件格式中,节是代码或数据的基本组织单位。添加新节时需要特别注意几个关键点:首先是节的对齐要求,这涉及到文件对齐(FileAlignment)和内存对齐(SectionAlignment)两个层面;其次是节的属性标志,这决定了该节在内存中的访问权限。对于可执行代码,我们需要同时设置读取和执行权限。
def add_section(section_name, content):
section_size = len(content)
last_section = pe.sections[-1]
# 计算符合对齐要求的地址
raw_offset = (last_section.PointerToRawData +
last_section.SizeOfRawData +
pe.OPTIONAL_HEADER.FileAlignment - 1) &
~(pe.OPTIONAL_HEADER.FileAlignment - 1)
virtual_addr = (last_section.VirtualAddress +
last_section.Misc_VirtualSize +
pe.OPTIONAL_HEADER.SectionAlignment - 1) &
~(pe.OPTIONAL_HEADER.SectionAlignment - 1)
# 设置节的属性
new_section.Characteristics = 0xE0000020 # R/X访问权限
0xE0000020这个标志位的设置:包含了IMAGE_SCN_CNT_CODE(可执行)、IMAGE_SCN_MEM_EXECUTE(允许执行)、IMAGE_SCN_MEM_READ(允许读取)等多个属性的组合。 这种组合确保了我们的代码可以在现代操作系统的内存保护机制下正常工作。
动态链接处理
接下来还有一个棘手的问题:我们需要在注入的代码中使用各种运行时函数,但又不能依赖传统的动态链接。这是因为我们的代码是直接注入到PE文件中的,没有正常的导入表支持。解决这个问题需要一些相当底层的技巧。
最关键的是获取kernel32.dll的基址。在64位Windows系统中,这涉及到一段的汇编代码:
__declspec(naked) static ULONGLONG GetKernel32Base() {
__asm__ __volatile__(
"movq %gs:0x60, %rax\n\t" // 获取PEB地址
"movq 0x18(%rax), %rax\n\t" // 获取PEB_LDR_DATA
"movq 0x30(%rax), %rax\n\t" // 获取InMemoryOrderModuleList
"movq (%rax), %rax\n\t" // 获取第一个条目(ntdll.dll)
"movq (%rax), %rax\n\t" // 获取第二个条目(kernel32.dll)
"movq 0x10(%rax), %rax\n\t" // 获取DllBase
"ret\n\t"
);
}
这段代码是Windows系统编程的一个经典技巧。 它利用了Windows进程内存布局的一个特性:通过GS段寄存器可以访问到线程环境块(TEB),进而获取到进程环境块(PEB)。在PEB中维护着已加载模块的链表,而kernel32.dll总是在固定的位置。这个技巧在shellcode编写中被广泛使用,因为它不依赖任何外部符号引用。
获取了kernel32.dll的基址后,就可以实现一个轻量级的函数解析器:
static FARPROC GetFunctionAddress(ULONGLONG moduleBase) {
auto *pDos = (IMAGE_DOS_HEADER *) moduleBase;
auto *pNt = (IMAGE_NT_HEADERS64 *) (moduleBase + pDos->e_lfanew);
auto *pExportDir = &pNt->OptionalHeader.DataDirectory[0];
auto *pExport = (IMAGE_EXPORT_DIRECTORY *) (moduleBase + pExportDir->VirtualAddress);
// ... 遍历导出表查找GetProcAddress函数 ...
}
这个实现展示了PE文件格式的精妙之处。DOS头、NT头、导出目录等数据结构形成了一个优雅的层次结构,使得我们可以在不依赖操作系统API的情况下实现符号解析。有趣的是,我们是在用手写的代码来模拟操作系统加载器的行为。
得到GetProcAddress函数后,我们就可以正常地加载msvcrt.dll并获取其他需要的函数了:
void initialize(Board *board, int startX, int startY) {
if (initialized) {
placeMines(board, startX, startY);
return;
}
ULONGLONG kernel32Base = GetKernel32Base();
auto GetProcAddress = (GetProcAddress_t) GetFunctionAddress(kernel32Base);
auto LoadLibraryA = (LoadLibraryA_t) GetProcAddress((HMODULE) kernel32Base, "LoadLibraryA");
// 加载运行时库
HMODULE msvcrt = LoadLibraryA("msvcrt.dll");
rand = (rand_t) GetProcAddress(msvcrt, "rand");
malloc = (malloc_t) GetProcAddress(msvcrt, "malloc");
// ... 获取其他需要的函数 ...
}
这段初始化代码的功能就算:在一个没有正常运行时环境的代码块中,逐步构建出了一个可用的运行时环境。这让我们能够在注入的代码中使用标准库(rand、malloc等等)函数,简化了后续的开发工作。
内存管理策略
在确保了基本的运行时函数可用之后,我们还需要特别注意内存管理。由于我们的代码是在一个受限环境中运行,任何内存泄漏都可能导致严重的问题。为此,我们采用了一种严格的手动内存管理策略:
// 创建mines数组示例
Array<Array<int> *> *mines = (Array<Array<int> *> *)malloc(sizeof(Array<Array<int> *>));
mines->size = width;
mines->capacity = width;
mines->growth = 0;
mines->data = (Array<int> **)malloc(width * sizeof(Array<int> *));
无猜算法实现
问题建模
扫雷游戏本质上可以看作一个约束满足问题(Constraint Satisfaction Problem, CSP)。每个已知数字格子都提供了一个关于其周围地雷数量的约束。如果一个局面是无猜的,那么这些约束应该足以推导出所有未知格子的状态。
布尔规划建模
给定一个布尔线性方程组:
$$ \begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \newline a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2 \newline \quad \vdots \newline a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m \newline \end{cases} $$
其中:
- $ x_i \in {0, 1} $(布尔变量)
- $ a_{ij} \in {0, 1} $(已知的布尔系数)
- $ b_i $ 是已知的正整数
将问题转化为布尔规划形式:每个未知格子表示为一个布尔变量$x_i$,其中:
- $x_i = 1$ 表示该格子是地雷
- $x_i = 0$ 表示该格子是安全的
对于每个已知数字n的格子,其周围的未知格子$x_1, x_2, …, x_k$满足约束: $x_1 + x_2 + … + x_k = n - m$
其中m是该数字周围已知地雷的数量,也就是我们可以使用的已知信息。
算法原型设计
在实现最终的C++版本之前,我们首先使用Python构建算法原型。Python的高级数据结构和简洁的语法让我们能够快速验证各种想法,并且容易进行算法调试。

核心求解器的Python实现
class MineSolver:
def __init__(self, mines: List[List[bool]]):
self.width = len(mines)
self.height = len(mines[0]) if self.width > 0 else 0
self.mines = mines
self.actions: List[Action] = []
self.assignments: Dict[Tuple[int, int], int] = {}
# 计算每个格子周围的地雷数
self.hints = [
[sum(mines[nx][ny] for nx, ny in self.get_neighbors(x, y))
for y in range(self.height)]
for x in range(self.width)
]
def get_neighbors(self, x: int, y: int) -> List[Tuple[int, int]]:
"""获取指定位置的所有相邻格子"""
neighbors = []
for dx in [-1, 0, 1]:
for dy in [-1, 0, 1]:
if dx == 0 and dy == 0:
continue
nx, ny = x + dx, y + dy
if 0 <= nx < self.width and 0 <= ny < self.height:
neighbors.append((nx, ny))
return neighbors
def get_unknown_neighbors(self, x: int, y: int) -> List[Tuple[int, int]]:
"""获取指定位置周围尚未确定的格子"""
return [(nx, ny) for nx, ny in self.get_neighbors(x, y)
if (nx, ny) not in self.assignments]
def get_clues(self) -> List[Clue]:
"""构建当前状态下的所有约束"""
clues = []
for x in range(self.width):
for y in range(self.height):
if (x, y) in self.assignments and self.assignments[(x, y)] == 0:
unknowns = self.get_unknown_neighbors(x, y)
if not unknowns:
continue
# 计算未确定格子中的地雷数
mine_count = self.hints[x][y] - sum(
1 for nx, ny in self.get_neighbors(x, y)
if self.assignments.get((nx, ny)) == 1
)
clues.append(Clue((x, y), unknowns, mine_count))
return clues
Python版本帮助我们理清了几个关键设计问题:
数据结构选择
- 使用字典存储已确定的格子状态
- 用元组表示坐标位置
- 将约束抽象为单独的
Clue类
约束表示
- 每个约束包含:中心格子位置、未知邻居列表、剩余地雷数
- 这种表示方式既直观又便于进行约束传播
约束传播的实现
def solve(self, start_x: int, start_y: int) -> List[Action]:
"""求解器的主要逻辑"""
# 初始化:标记起始点为安全
self.assignments[(start_x, start_y)] = 0
self.actions.append(Action(start_x, start_y, False))
# 反复应用约束传播直到无法推导出新信息
while self.propagate_constraints():
pass
return self.actions
def propagate_constraints(self) -> bool:
"""约束传播的具体实现"""
progress = False
constraints = self.get_clues()
for eq in constraints:
unknowns = eq.unknowns
mines_left = eq.mines
if len(unknowns) == mines_left:
# 所有未知格子都是地雷
for x, y in unknowns:
if self.assignments.get((x, y)) != 1:
self.assignments[(x, y)] = 1
self.actions.append(Action(x, y, True))
progress = True
continue
if mines_left == 0:
# 所有未知格子都是安全的
for x, y in unknowns:
if self.assignments.get((x, y)) != 0:
self.assignments[(x, y)] = 0
self.actions.append(Action(x, y, False))
progress = True
continue
Python原型的实现帮助我们发现:
- 约束传播算法的效率主要受约束数量的影响
- 新信息的产生往往形成链式反应
- 部分约束可能在多轮传播中重复使用
这些发现直接影响了C++版本的设计决策:
- 使用数组替代字典,提高访问效率
- 实现专门的内存池,避免频繁的内存分配
- 添加约束缓存机制,减少重复计算

约束传播算法
虽然有很多SAT求解器可以使用,但是我们的代码并不能很好地使用共享库。如果我们使用静态编译,会导致最终的可执行文件体积增大很多,这是非常不划算的。 并且考虑到扫雷游戏的特殊性,我们可以实现一个更高效的专用算法。 核心思路是利用约束传播(Constraint Propagation)来逐步推导出确定的格子。
bool MineSolver_propagate_constraints(MineSolver *solver) {
bool progress = false;
Array<Clue> *constraints = MineSolver_get_clues(solver);
for (int i = 0; i < constraints->size; ++i) {
Clue *eq = &constraints->data[i];
Array<Position> *unknowns = eq->unknowns;
int mines_left = eq->mines;
// 约束1:剩余未知格子数等于剩余地雷数
if (mines_left == unknowns->size) {
for (int j = 0; j < unknowns->size; ++j) {
Position pos = unknowns->data[j];
if (solver->assignments[pos.x][pos.y] != 1) {
solver->assignments[pos.x][pos.y] = 1;
solver->actions->Add(Action{pos.x, pos.y, true});
progress = true;
}
}
continue;
}
// 约束2:剩余地雷数为0
if (mines_left == 0) {
for (int j = 0; j < unknowns->size; ++j) {
Position pos = unknowns->data[j];
solver->assignments[pos.x][pos.y] = 0;
solver->actions->Add(Action{pos.x, pos.y, false});
progress = true;
}
continue;
}
// 约束3:子集推理
for (int k = 0; k < constraints->size; ++k) {
if (k == i) continue;
Clue *other_eq = &constraints->data[k];
// 检查是否构成子集关系...
这段代码实现了三种基本的推理规则:
- 当剩余未知格数等于剩余地雷数时,所有未知格都是地雷
- 当剩余地雷数为0时,所有未知格都是安全的
- 当两个约束之间存在子集关系时,可以通过差集推理得到新的确定格子
子集推理的实现
子集推理是算法中最复杂但也最强大的部分。考虑两个相邻的数字格子A和B,如果A的未知邻居是B的未知邻居的子集,那么可以通过它们的差集得到新的信息:
if (is_subset) {
Array<Position> *difference = get_difference(unknowns, other_eq->unknowns);
int mine_difference = eq->mines - other_eq->mines;
if (mine_difference == difference->size) {
// 差集中所有格子都是地雷
mark_all_as_mines(difference);
} else if (mine_difference == 0) {
// 差集中所有格子都是安全的
mark_all_as_safe(difference);
}
}
地雷生成算法
有了判定机制后,我们可以实现一个保证无猜的地雷生成算法:
void placeMines(Board *board, int startX, int startY) {
int width = board->width;
int height = board->height;
int mineCount = board->mineCount;
int oldRandSeed = board->randSeed;
srand(board->randSeed);
constexpr int maxAttempts = 500;
for (int attempts = 0; attempts < maxAttempts; attempts++) {
// 随机放置地雷
clear_board(board);
place_random_mines(board, mineCount, startX, startY);
// 验证是否可解
MineSolver solver;
MineSolver_init(&solver, convert_to_solver_format(board), width, height);
Array<Action> *actions = MineSolver_solve(&solver, startX, startY);
if (actions->size == width * height) {
// 找到有效解,清理资源并返回
cleanup_resources(&solver);
break;
}
// 清理本次尝试的资源
cleanup_resources(&solver);
}
srand(oldRandSeed);
}
采用"生成-验证"的思路:随机生成一个地雷布局,然后使用求解器验证是否可以通过纯逻辑推理完成。如果不能完全推理,就重新生成,直到找到一个满足条件的布局。
在测试中,大部分情况下都能在前几次尝试内找到合适的布局。 只有一些极端情况,比如10x10的地图需要放置89个类,除去初始位置的3x3区域,还有一个空白格子是随机的,这种情况下,显然只有当空白格子与初始区域相邻时才可解。 所以通过限制最大尝试次数,可以在保证游戏质量的同时,控制地图生成的时间开销,避免上述情况下的超时。 在实际使用中,最大规格的地图(30x24, 668)都能在无感的时间内生成,与完全随机的地图生成相比,没有任何延迟,常玩的高级难度就更不用说了。

如图所示,经过改造的扫雷游戏能够保证每一步都有明确的逻辑推理路径,不再需要靠运气来完成游戏,提供了一个纯粹的游戏体验。
完整代码请参考我的GitHub仓库:minesweeper