In the classic Minesweeper game, players often encounter a frustrating situation: even after applying all possible logical deduction techniques, they still have to rely purely on luck to choose their next move. This “forced guessing” design has long been one of the most criticized flaws in Minesweeper. While there are already some no-guess versions of Minesweeper available, I have a particular fondness for the classic interface of the Windows 7 version. This sparked an idea: could we transform it into a true “logic game” while preserving the original interface?
Reverse Engineering Analysis
Since we cannot access the source code of the original Minesweeper, we need to understand and modify the game logic through reverse engineering. Fortunately, this game comes with debug symbols (PDB files), which greatly simplifies our analysis work.
Initial Analysis with IDA
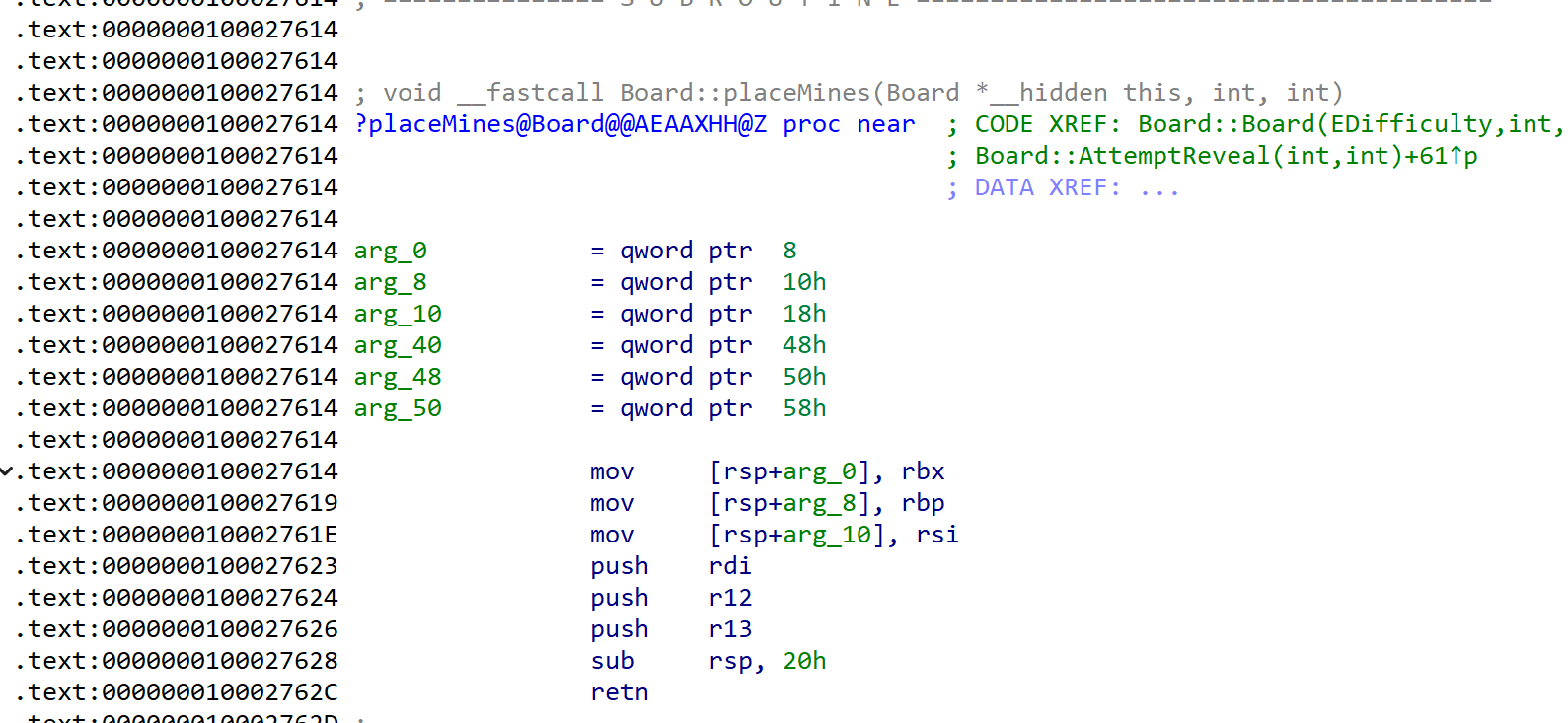
Opening Minesweeper.exe with IDA Pro, the IDE automatically downloaded the corresponding PDB file. Through symbol information, we can directly locate the key function Board::Board:
__int64 __fastcall Board::Board(__int64 a1, int a2, int a3, int a4, int a5, int a6, int a7, int a8, char a9)
{
// ... initialization code omitted ...
if ( *(_DWORD *)(a1 + 8) > *(_DWORD *)(a1 + 12) * *(_DWORD *)(a1 + 16) - 9 )
{
v22 = Str::Str((Str *)v25, L"Too many mines for tile count");
LOBYTE(v23) = 1;
StrErr(v22, v23);
*(_DWORD *)(a1 + 8) = *(_DWORD *)(a1 + 12) * *(_DWORD *)(a1 + 16) - 9;
}
return a1;
}
By analyzing the disassembled code, we can infer the main structure of the Board class. Notably, the code includes a boundary check ensuring that the number of mines doesn’t exceed (width * height - 9), where “-9” corresponds to the 3×3 blank area that needs to be reserved for the first click.
In-depth Analysis of Mine Placement Algorithm
Further analysis reveals that the core mine placement logic is in the Board::placeMines function. After analysis and code beautification, its basic logic is as follows:
void Board::placeMines(int firstX, int firstY) {
// Save current random seed state
unsigned int oldSeed = Seed;
srand(this->randSeed);
Seed = this->randSeed;
// Create list of possible mine positions
Array<int>* availablePositions = new Array<int>();
// Collect all legal mine placement positions
// Exclude 3×3 range of first click
for(int i = 0; i < height * width; i++) {
int x = i % width;
int y = i / width;
int dx = x - firstX;
int dy = y - firstY;
if(abs(dx) > 1 || abs(dy) > 1) {
availablePositions->Add(i);
}
}
// Randomly select specified number of positions to place mines
while(minePositions->size < mineCount && availablePositions->size > 0) {
int randomIndex = rand() % availablePositions->size;
int position = availablePositions->data[randomIndex];
minePositions->Add(position);
// ... remove selected position from available positions list ...
}
// Restore random seed
srand(oldSeed);
Seed = oldSeed;
}
Analyzing this code, we can see that:
- The game uses a linear congruential random number generator
- Mine placement uses a simple random sampling strategy
- The first click safety zone is implemented by excluding corresponding positions beforehand
While this random placement strategy ensures basic playability, it doesn’t consider whether the board can be solved through pure logical deduction, which is the root cause of “forced guessing” situations.
Static Patch Solution Design
The most straightforward modification would be using DLL injection technology, but this method requires an additional loader, introduces unnecessary startup delay, and complicates the startup process beyond simply double-clicking the exe file. In pursuit of a more elegant solution, I decided to use static patching to directly modify the code section of the executable.
First, let’s try the simplest modification: changing the placeMines function to return directly, to test if our patching mechanism works:
def va2foffset(va):
"""Convert virtual address to file offset"""
image_base = pe.OPTIONAL_HEADER.ImageBase
rva = va - image_base
for section in pe.sections:
if section.VirtualAddress <= rva < section.VirtualAddress + section.SizeOfRawData:
return (rva - section.VirtualAddress) + section.PointerToRawData
return None
# Locate the start position of placeMines function
place_mines_offset = va2foffset(0x100027614)
# Inject a simple return instruction
encoding, _ = ks.asm('ret', as_bytes=True)
with open(target_path, 'r+b') as f:
f.seek(place_mines_offset)
f.write(encoding)
Testing the game, we indeed got a completely mine-free board:

We can control the mine distribution in the game through static patching.

This initial test confirmed that our patching mechanism is feasible. However, to implement a true no-guess Minesweeper algorithm, we need a larger code space. The existing placeMines function space is clearly insufficient to accommodate complex algorithm logic.
Code Section Patching and Memory Management
PE File Structure Extension
After confirming that the basic patching mechanism works, our first technical challenge is how to inject enough code space into the PE file. The original placeMines function obviously cannot accommodate our no-guess algorithm implementation. The most natural solution is to add a new section. This approach is not only elegant but also maintains the integrity of the original code section.
In the PE file format, sections are the basic organizational units for code or data. When adding new sections, several key points need special attention: first is the alignment requirements, which involve both file alignment (FileAlignment) and memory alignment (SectionAlignment); second is the section attribute flags, which determine the access permissions of the section in memory. For executable code, we need to set both read and execute permissions.
def add_section(section_name, content):
section_size = len(content)
last_section = pe.sections[-1]
# Calculate addresses that meet alignment requirements
raw_offset = (last_section.PointerToRawData +
last_section.SizeOfRawData +
pe.OPTIONAL_HEADER.FileAlignment - 1) &
~(pe.OPTIONAL_HEADER.FileAlignment - 1)
virtual_addr = (last_section.VirtualAddress +
last_section.Misc_VirtualSize +
pe.OPTIONAL_HEADER.SectionAlignment - 1) &
~(pe.OPTIONAL_HEADER.SectionAlignment - 1)
# Set section attributes
new_section.Characteristics = 0xE0000020 # R/X access permissions
The flag setting of 0xE0000020: includes a combination of multiple attributes including IMAGE_SCN_CNT_CODE (executable), IMAGE_SCN_MEM_EXECUTE (allow execution), IMAGE_SCN_MEM_READ (allow reading), etc. This combination ensures our code can work normally under modern operating systems’ memory protection mechanisms.
Dynamic Linking Handling
Next comes a tricky problem: we need to use various runtime functions in our injected code, but we can’t rely on traditional dynamic linking. This is because our code is directly injected into the PE file without normal import table support. Solving this problem requires some quite low-level tricks.
The most crucial part is obtaining the base address of kernel32.dll. On 64-bit Windows systems, this involves a piece of assembly code:
__declspec(naked) static ULONGLONG GetKernel32Base() {
__asm__ __volatile__(
"movq %gs:0x60, %rax\n\t" // Get PEB address
"movq 0x18(%rax), %rax\n\t" // Get PEB_LDR_DATA
"movq 0x30(%rax), %rax\n\t" // Get InMemoryOrderModuleList
"movq (%rax), %rax\n\t" // Get first entry (ntdll.dll)
"movq (%rax), %rax\n\t" // Get second entry (kernel32.dll)
"movq 0x10(%rax), %rax\n\t" // Get DllBase
"ret\n\t"
);
}
This code is a classic trick in Windows system programming. It utilizes a feature of Windows process memory layout: through the GS segment register, we can access the Thread Environment Block (TEB), and thus get the Process Environment Block (PEB). The PEB maintains a list of loaded modules, and kernel32.dll is always at a fixed position. This trick is widely used in shellcode writing because it doesn’t rely on any external symbol references.
After obtaining the base address of kernel32.dll, we can implement a lightweight function resolver:
static FARPROC GetFunctionAddress(ULONGLONG moduleBase) {
auto *pDos = (IMAGE_DOS_HEADER *) moduleBase;
auto *pNt = (IMAGE_NT_HEADERS64 *) (moduleBase + pDos->e_lfanew);
auto *pExportDir = &pNt->OptionalHeader.DataDirectory[0];
auto *pExport = (IMAGE_EXPORT_DIRECTORY *) (moduleBase + pExportDir->VirtualAddress);
// ... traverse export table to find GetProcAddress function ...
}
This implementation demonstrates the elegance of the PE file format. DOS header, NT header, export directory, and other data structures form an elegant hierarchical structure, allowing us to implement symbol resolution without relying on operating system APIs. Interestingly, we are using handwritten code to simulate the behavior of the operating system loader.
After getting the GetProcAddress function, we can normally load msvcrt.dll and obtain other needed functions:
void initialize(Board *board, int startX, int startY) {
if (initialized) {
placeMines(board, startX, startY);
return;
}
ULONGLONG kernel32Base = GetKernel32Base();
auto GetProcAddress = (GetProcAddress_t) GetFunctionAddress(kernel32Base);
auto LoadLibraryA = (LoadLibraryA_t) GetProcAddress((HMODULE) kernel32Base, "LoadLibraryA");
// Load runtime library
HMODULE msvcrt = LoadLibraryA("msvcrt.dll");
rand = (rand_t) GetProcAddress(msvcrt, "rand");
malloc = (malloc_t) GetProcAddress(msvcrt, "malloc");
// ... get other needed functions ...
}
The functionality of this initialization code is: in a code block without a normal runtime environment, gradually building up a usable runtime environment. This allows us to use standard library functions (rand, malloc, etc.) in the injected code, simplifying subsequent development work.
Memory Management Strategy
After ensuring basic runtime functions are available, we need to pay special attention to memory management. Since our code runs in a restricted environment, any memory leaks could lead to serious problems. For this, we adopted a strict manual memory management strategy:
// Example of creating mines array
Array<Array<int> *> *mines = (Array<Array<int> *> *)malloc(sizeof(Array<Array<int> *>));
mines->size = width;
mines->capacity = width;
mines->growth = 0;
mines->data = (Array<int> **)malloc(width * sizeof(Array<int> *));
No-Guess Algorithm Implementation
Problem Modeling
Minesweeper can essentially be viewed as a Constraint Satisfaction Problem (CSP). Each known number cell provides a constraint about the number of mines in its surroundings. If a board is no-guess, these constraints should be sufficient to deduce the state of all unknown cells.
Boolean Programming Modeling
Given a system of Boolean linear equations:
$$ \begin{cases} a_{11}x_1 + a_{12}x_2 + \dots + a_{1n}x_n = b_1 \newline a_{21}x_1 + a_{22}x_2 + \dots + a_{2n}x_n = b_2 \newline \quad \vdots \newline a_{m1}x_1 + a_{m2}x_2 + \dots + a_{mn}x_n = b_m \newline \end{cases} $$
where:
- $ x_i \in {0, 1} $ (Boolean variables)
- $ a_{ij} \in {0, 1} $ (known Boolean coefficients)
- $ b_i $ are known positive integers
Converting the problem into Boolean programming form: each unknown cell is represented as a Boolean variable $x_i$, where:
- $x_i = 1$ indicates the cell is a mine
- $x_i = 0$ indicates the cell is safe
For each known number n cell, its surrounding unknown cells $x_1, x_2, …, x_k$ satisfy the constraint: $x_1 + x_2 + … + x_k = n - m$
where m is the number of known mines around that number, which is the known information we can use.
Algorithm Prototype Design
Before implementing the final C++ version, we first built the algorithm prototype using Python. Python’s high-level data structures and concise syntax allowed us to quickly validate various ideas and easily debug the algorithm.

Python Implementation of Core Solver
class MineSolver:
def __init__(self, mines: List[List[bool]]):
self.width = len(mines)
self.height = len(mines[0]) if self.width > 0 else 0
self.mines = mines
self.actions: List[Action] = []
self.assignments: Dict[Tuple[int, int], int] = {}
# Calculate number of mines around each cell
self.hints = [
[sum(mines[nx][ny] for nx, ny in self.get_neighbors(x, y))
for y in range(self.height)]
for x in range(self.width)
]
def get_neighbors(self, x: int, y: int) -> List[Tuple[int, int]]:
"""Get all adjacent cells for the specified position"""
neighbors = []
for dx in [-1, 0, 1]:
for dy in [-1, 0, 1]:
if dx == 0 and dy == 0:
continue
nx, ny = x + dx, y + dy
if 0 <= nx < self.width and 0 <= ny < self.height:
neighbors.append((nx, ny))
return neighbors
def get_unknown_neighbors(self, x: int, y: int) -> List[Tuple[int, int]]:
"""Get undetermined cells around the specified position"""
return [(nx, ny) for nx, ny in self.get_neighbors(x, y)
if (nx, ny) not in self.assignments]
def get_clues(self) -> List[Clue]:
"""Build all constraints for the current state"""
clues = []
for x in range(self.width):
for y in range(self.height):
if (x, y) in self.assignments and self.assignments[(x, y)] == 0:
unknowns = self.get_unknown_neighbors(x, y)
if not unknowns:
continue
# Calculate number of mines in undetermined cells
mine_count = self.hints[x][y] - sum(
1 for nx, ny in self.get_neighbors(x, y)
if self.assignments.get((nx, ny)) == 1
)
clues.append(Clue((x, y), unknowns, mine_count))
return clues
The Python version helped us clarify several key design issues:
Data Structure Selection
- Using dictionary to store determined cell states
- Using tuples to represent coordinates
- Abstracting constraints into a separate
Clueclass
Constraint Representation
- Each constraint includes: center cell position, list of unknown neighbors, remaining mine count
- This representation is both intuitive and conducive to constraint propagation
Implementation of Constraint Propagation
def solve(self, start_x: int, start_y: int) -> List[Action]:
"""Main solver logic"""
# Initialize: mark starting point as safe
self.assignments[(start_x, start_y)] = 0
self.actions.append(Action(start_x, start_y, False))
# Repeatedly apply constraint propagation until no new information can be deduced
while self.propagate_constraints():
pass
return self.actions
def propagate_constraints(self) -> bool:
"""Specific implementation of constraint propagation"""
progress = False
constraints = self.get_clues()
for eq in constraints:
unknowns = eq.unknowns
mines_left = eq.mines
if len(unknowns) == mines_left:
# All unknown cells are mines
for x, y in unknowns:
if self.assignments.get((x, y)) != 1:
self.assignments[(x, y)] = 1
self.actions.append(Action(x, y, True))
progress = True
continue
if mines_left == 0:
# All unknown cells are safe
for x, y in unknowns:
if self.assignments.get((x, y)) != 0:
self.assignments[(x, y)] = 0
self.actions.append(Action(x, y, False))
progress = True
continue
The Python prototype implementation helped us discover:
- The efficiency of the constraint propagation algorithm is mainly affected by the number of constraints
- The generation of new information often forms a chain reaction
- Some constraints may be reused across multiple rounds of propagation
These findings directly influenced the design decisions for the C++ version:
- Using arrays instead of dictionaries to improve access efficiency
- Implementing a dedicated memory pool to avoid frequent memory allocation
- Adding a constraint caching mechanism to reduce repeated calculations

Constraint Propagation Algorithm
Although many SAT solvers are available, our code cannot effectively use shared libraries. If we use static compilation, it would significantly increase the final executable size, which is very inefficient. Moreover, considering the special nature of Minesweeper, we can implement a more efficient specialized algorithm. The core idea is to use Constraint Propagation to gradually deduce determined cells.
bool MineSolver_propagate_constraints(MineSolver *solver) {
bool progress = false;
Array<Clue> *constraints = MineSolver_get_clues(solver);
for (int i = 0; i < constraints->size; ++i) {
Clue *eq = &constraints->data[i];
Array<Position> *unknowns = eq->unknowns;
int mines_left = eq->mines;
// Constraint 1: Number of remaining unknown cells equals remaining mines
if (mines_left == unknowns->size) {
for (int j = 0; j < unknowns->size; ++j) {
Position pos = unknowns->data[j];
if (solver->assignments[pos.x][pos.y] != 1) {
solver->assignments[pos.x][pos.y] = 1;
solver->actions->Add(Action{pos.x, pos.y, true});
progress = true;
}
}
continue;
}
// Constraint 2: Number of remaining mines is 0
if (mines_left == 0) {
for (int j = 0; j < unknowns->size; ++j) {
Position pos = unknowns->data[j];
solver->assignments[pos.x][pos.y] = 0;
solver->actions->Add(Action{pos.x, pos.y, false});
progress = true;
}
continue;
}
// Constraint 3: Subset inference
for (int k = 0; k < constraints->size; ++k) {
if (k == i) continue;
Clue *other_eq = &constraints->data[k];
// Check for subset relationship...
This code implements three basic inference rules:
- When the number of remaining unknown cells equals the number of remaining mines, all unknown cells are mines
- When the number of remaining mines is 0, all unknown cells are safe
- When there’s a subset relationship between two constraints, new determined cells can be deduced through set difference
Subset Inference Implementation
Subset inference is the most complex but also most powerful part of the algorithm. Consider two adjacent number cells A and B, if A’s unknown neighbors are a subset of B’s unknown neighbors, then new information can be obtained through their set difference:
if (is_subset) {
Array<Position> *difference = get_difference(unknowns, other_eq->unknowns);
int mine_difference = eq->mines - other_eq->mines;
if (mine_difference == difference->size) {
// All cells in the difference set are mines
mark_all_as_mines(difference);
} else if (mine_difference == 0) {
// All cells in the difference set are safe
mark_all_as_safe(difference);
}
}
Mine Generation Algorithm
With the determination mechanism in place, we can implement a mine generation algorithm that guarantees no guessing:
void placeMines(Board *board, int startX, int startY) {
int width = board->width;
int height = board->height;
int mineCount = board->mineCount;
int oldRandSeed = board->randSeed;
srand(board->randSeed);
constexpr int maxAttempts = 500;
for (int attempts = 0; attempts < maxAttempts; attempts++) {
// Randomly place mines
clear_board(board);
place_random_mines(board, mineCount, startX, startY);
// Verify solvability
MineSolver solver;
MineSolver_init(&solver, convert_to_solver_format(board), width, height);
Array<Action> *actions = MineSolver_solve(&solver, startX, startY);
if (actions->size == width * height) {
// Found valid solution, clean up resources and return
cleanup_resources(&solver);
break;
}
// Clean up resources for this attempt
cleanup_resources(&solver);
}
srand(oldRandSeed);
}
Using a “generate-and-verify” approach: randomly generate a mine layout, then use the solver to verify if it can be completed through pure logical reasoning. If it cannot be fully deduced, generate again until finding a layout that meets the conditions.
In testing, suitable layouts can usually be found within the first few attempts. Only in some extreme cases, such as when placing 89 mines on a 10x10 map, excluding the initial 3x3 area, where one blank cell is random, the solution is obviously only possible when the blank cell is adjacent to the initial area. Therefore, by limiting the maximum number of attempts, we can control the map generation time while ensuring game quality, avoiding timeouts in such cases. In practical use, even maps of maximum size (30x24, 668) can be generated in imperceptible time, with no delay compared to completely random map generation, let alone the commonly played expert difficulty.

As shown in the image, the modified Minesweeper game ensures that every step has a clear logical deduction path, no longer requiring luck to complete the game, providing a pure gaming experience.
For the complete code, please refer to my GitHub repository: minesweeper